Cantilever Beam: Influence of Element Type and Layers
Written on May 7th, 2022 by Joseph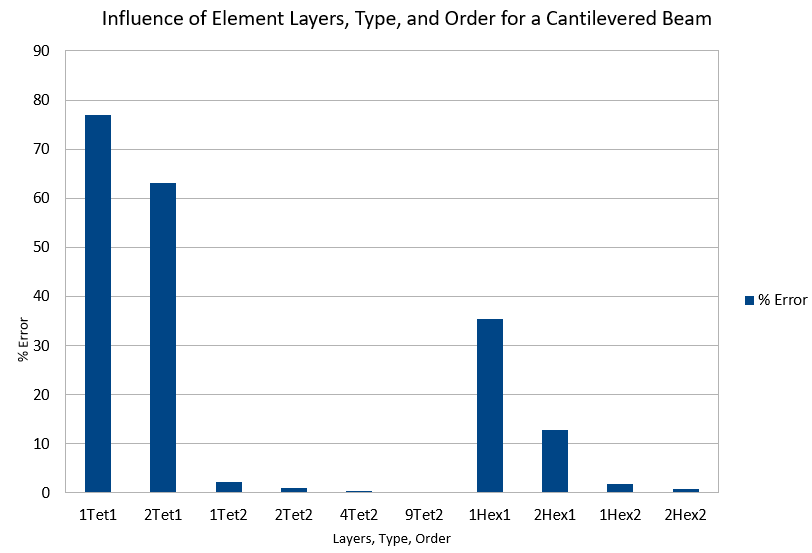
There are many choices to make when creating a mesh for a finite element model. These include the element type, the element order, and the number of layers to be utilized in the model. I wanted to explore these parameters for a cantilever beam to better understand how they affect the accuracy. I explored the following:
- Element type
- Hexahedral
- Tetrahedral
- Element order
- 1st order
- 2nd order
- Layers (1, 2, 4, 9)
The computations were performed with Code Aster according to the following comm file.
DEBUT(LANG='EN')
mesh = LIRE_MAILLAGE(UNITE=20)
model = AFFE_MODELE(AFFE=_F(MODELISATION=('3D', ),
PHENOMENE='MECANIQUE',
TOUT='OUI'),
MAILLAGE=mesh)
mater = DEFI_MATERIAU(ELAS=_F(E=200000.0,
NU=0.3))
fieldmat = AFFE_MATERIAU(AFFE=_F(MATER=(mater, ),
TOUT='OUI'),
MAILLAGE=mesh)
load = AFFE_CHAR_MECA(DDL_IMPO=_F(DX=0.0,
DY=0.0,
DZ=1.0,
GROUP_MA=('fixZFace', )),
FORCE_FACE=_F(FY=2.0,
GROUP_MA=('load', )),
MODELE=model)
reslin = MECA_STATIQUE(CHAM_MATER=fieldmat,
EXCIT=_F(CHARGE=load),
MODELE=model)
IMPR_RESU(FORMAT='MED',
RESU=_F(RESULTAT=reslin),
UNITE=80)
FIN()
The results were compared based on the amount of deflection at the end of the beam as compared with the analytical solution.

First order tetrahedral elements were extremely inaccurate. Even with two layers, the error was in excess of 60%. First order hexahedral elements perfomed better, with error approaching 10% for two layers. Second order tetrahedral elements performed quite well with one layer at 2.2% and two layers just under 1%. The errors continued to decrease and at nine layers the error had decreased to 0.25%. The second order hexahedral elements also performed very well with less than 1% error with two layers. They did better than their tetrahedral counterparts, but they are also more expensive computationally. In summary, where deflections (and stresses) are important, second order elements should typically be selected for better accuracy.