Cantilever Beam: Calculix vs Code Aster
Written on April 29th, 2022 by Joseph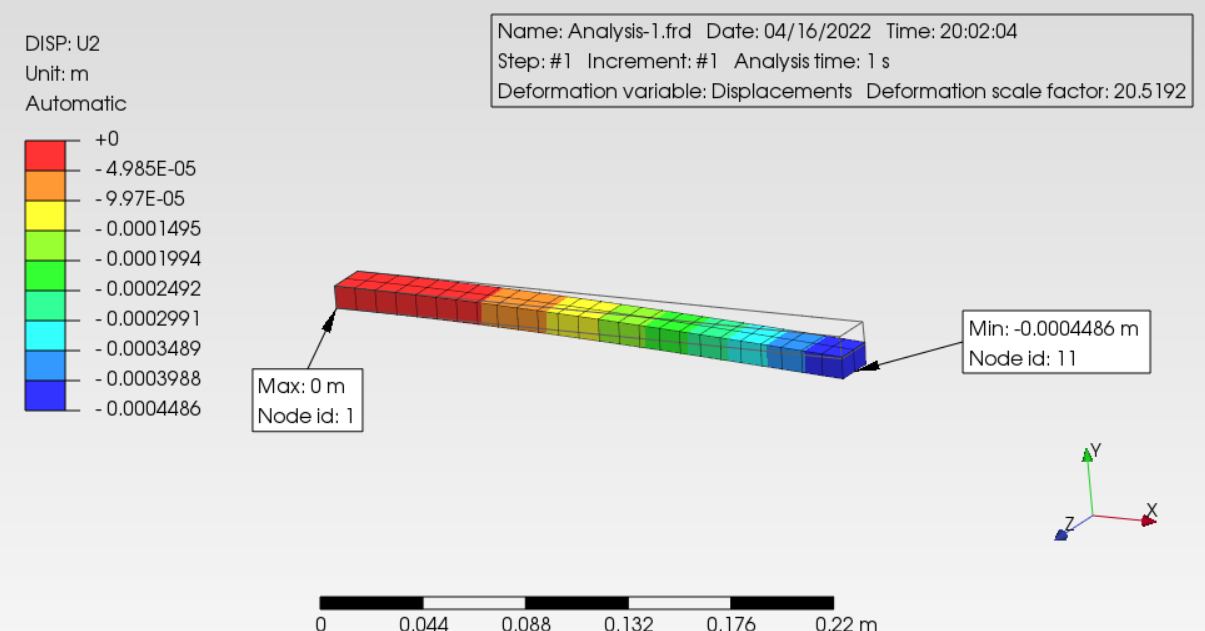
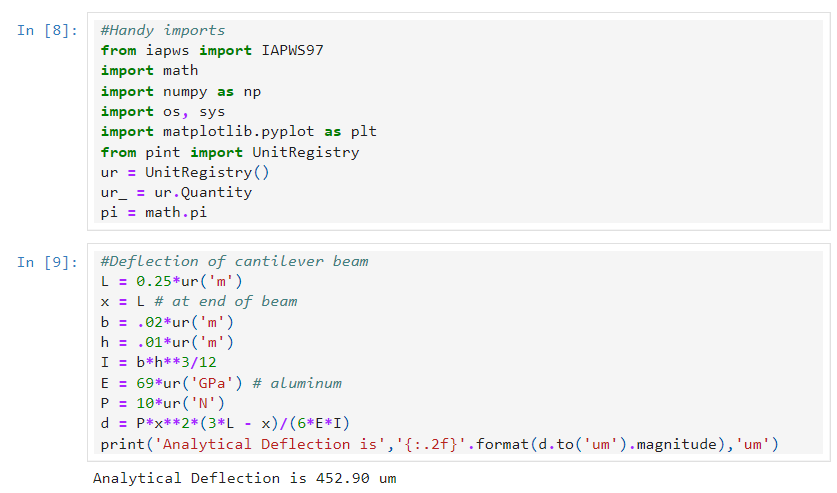
I am interested in making a number of comparisons to validate different finite element and finite volume approaches/softwares. This post will compare the results from two open source FEA packages called Calculix and Code Aster. The first step is to calculate the deflection using an analytical approach for comparison to the numerical approaches. For this comparison, I will look at a cantilevered beam. The beam is fixed at one end and all of the loading is applied as a point load at the other.
I will first solve this with Calculix using PrePoMax as a convenient interface to set up the problem. The mesh was generated with one layer of second order hex elements using Salome. More layers would be needed for the solution to be independent of the mesh, but this is fine for comparing the results of the two softwares to each other.

Here is the abbreviated step file used as input for CCX.
**
** Heading +++++++++++++++++++++++++++++++++++++++++++++++++
*Heading
Hash: OzciZ7SO, Date: 04/23/2022, Unit system: M_KG_S_C
** Nodes +++++++++++++++++++++++++++++++++++++++++++++++++++
*Node
... hidden data ...
** Elements ++++++++++++++++++++++++++++++++++++++++++++++++
*Element, Type=C3D20, Elset=Solid_part-1
... hidden data ...
** Node sets +++++++++++++++++++++++++++++++++++++++++++++++
*Nset, Nset=Internal-1_fix
... hidden data ...
*Nset, Nset=Internal-1_load
... hidden data ...
*Nset, Nset=Internal_Selection-1_Fixed-1
... hidden data ...
*Nset, Nset=Internal-1_Internal_Selection-1_Surface_traction-1
... hidden data ...
** Element sets ++++++++++++++++++++++++++++++++++++++++++++
*Elset, Elset=alum
... hidden data ...
*Elset, Elset=Internal-1_fix_S1
... hidden data ...
*Elset, Elset=Internal-1_load_S2
... hidden data ...
*Elset, Elset=Internal-1_Internal_Selection-1_Surface_traction-1_S2
... hidden data ...
** Surfaces ++++++++++++++++++++++++++++++++++++++++++++++++
*Surface, Name=fix, Type=Element
Internal-1_fix_S1, S1
*Surface, Name=load, Type=Element
Internal-1_load_S2, S2
*Surface, Name=Internal_Selection-1_Surface_traction-1, Type=Element
Internal-1_Internal_Selection-1_Surface_traction-1_S2, S2
** Materials +++++++++++++++++++++++++++++++++++++++++++++++
*Material, Name=aluminum
*Elastic
69000000000, 0.3
*Solid section, Elset=alum, Material=aluminum
** Step-1 ++++++++++++++++++++++++++++++++++++++++++++++++++
*Step
*Static
** Boundary conditions +++++++++++++++++++++++++++++++++++++
*Boundary, op=New
** Name: Fixed-1
*Boundary
Internal_Selection-1_Fixed-1, 1, 6, 0
** Loads +++++++++++++++++++++++++++++++++++++++++++++++++++
*Cload, op=New
*Dload, op=New
** Name: Surface_traction-1
*Cload
5, 2, 4.16666667E-001
7, 2, 4.16666667E-001
12, 2, 8.33333333E-001
11, 2, 8.33333333E-001
165, 2, -1.66666667E+000
167, 2, -1.66666667E+000
270, 2, -3.33333333E+000
164, 2, -1.66666667E+000
8, 2, 4.16666667E-001
6, 2, 4.16666667E-001
166, 2, -1.66666667E+000
168, 2, -1.66666667E+000
163, 2, -1.66666667E+000
*Node file
RF, U
*El file
S, E
** End step ++++++++++++++++++++++++++++++++++++++++++++++++
*End step
Results of the deflection are shown here.

The next approach was to use Code Aster to solve the same problem. Here is the comm file from Code Aster.
DEBUT(LANG='FR')
mesh = LIRE_MAILLAGE(UNITE=20)
model = AFFE_MODELE(AFFE=_F(MODELISATION=('3D', ),
PHENOMENE='MECANIQUE',
TOUT='OUI'),
MAILLAGE=mesh)
mater = DEFI_MATERIAU(ELAS=_F(E=69000000000.0,
NU=0.3))
fieldmat = AFFE_MATERIAU(AFFE=_F(MATER=(mater, ),
TOUT='OUI'),
MODELE=model)
fix = AFFE_CHAR_MECA(DDL_IMPO=_F(DX=0.0,
DY=0.0,
DZ=0.0,
GROUP_MA=('fix', )),
MODELE=model)
load1 = AFFE_CHAR_MECA(FORCE_FACE=_F(FY=-50000.0,
GROUP_MA=('load', )),
MODELE=model)
reslin = MECA_STATIQUE(CHAM_MATER=fieldmat,
EXCIT=(_F(CHARGE=load1),
_F(CHARGE=fix)),
MODELE=model)
IMPR_RESU(FORMAT='MED',
RESU=_F(MAILLAGE=mesh,
RESULTAT=reslin),
UNITE=2)
FIN()
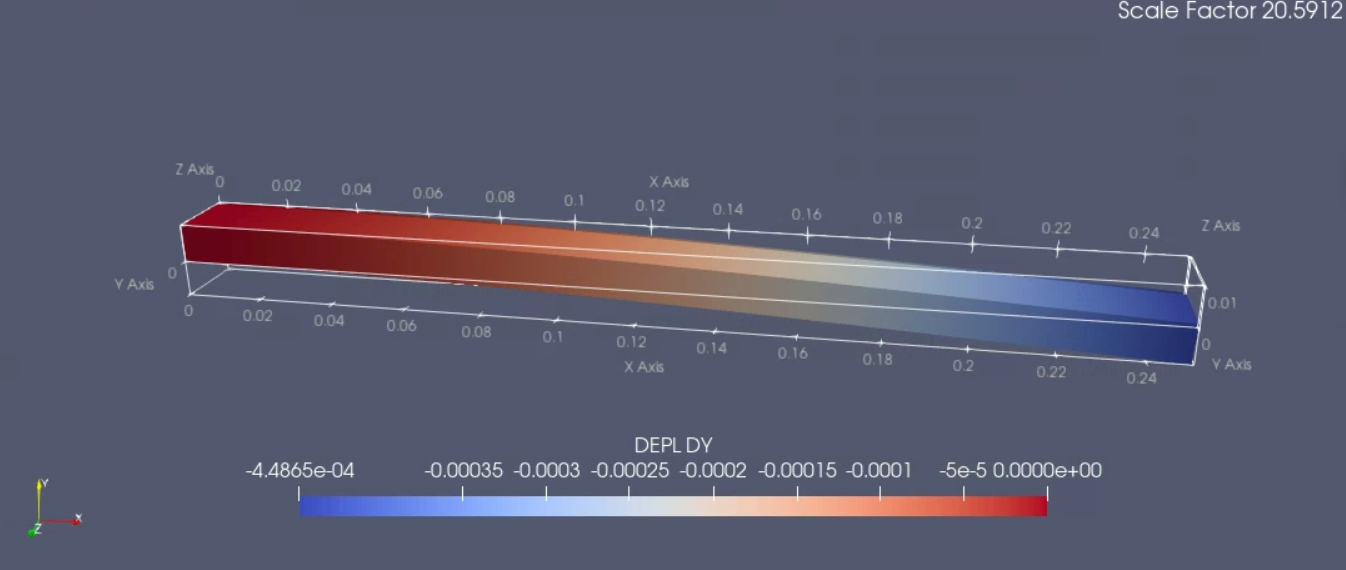
Analytical Deflection 452.90 um
Calculix Deflection is 448.6 um
Code Aster Deflection is 448.7 um
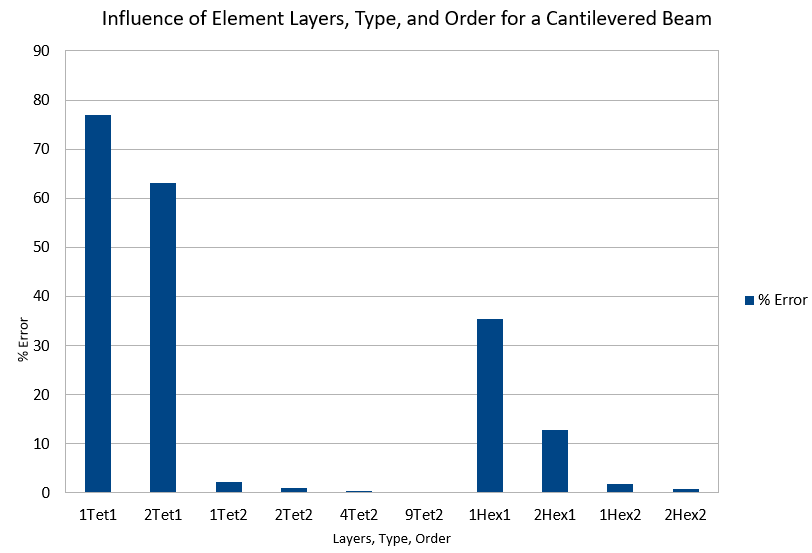
Both solvers have excellent agreement with each other and are within 1% of the analytical solution. This is good considering the mesh is only one layer thick. In another post I will explore how the solution changes with different element types and number layers.